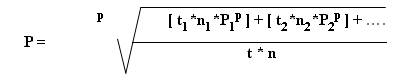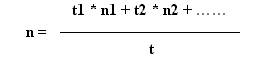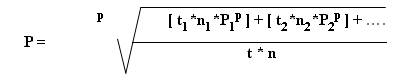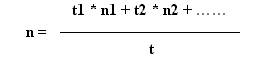ESTIMATION DE LA DUREE DE VIE DE ROULEMENTS
Durée de vie nominale d'un roulement
La durée de vie nominale des roulements ( avec une fiabilité de 90 % ) s'exprime par les formules :
L 10 = ( C / P ) n			ou	L 10 H = ( L 10 . 106 ) / ( 60 . N )
Avec :	L 10	Durée de vie du roulement en millions de tours
	C	Charge dynamique de base
	P	Charge équivalente exercée sur le roulement
	n	3	pour les roulements et butées à billes
		10/3	pour les roulements et butées à rouleaux
	N	Vitesse de rotation en tr / min.
Durée de vie nominale corrigée d'un roulement
La durée de vie nominale corrigée s'exprime par la formule : L n = a1 . L 10 avec a1 : Facteur de correction de durée pour la fiabilité du calcul.
Fiabilité en %			Désignation : Ln			a1
90			L 10			1
95			L 5			0.62
96			L 4			0.53
97			L 3			0.44
98			L 2			0.33
99			L 1			0.21
En cas de charge extrêmement élevées : P > 0.5 C ou P > Co ( prendre la valeur la plus faible ), il convient de consulter le fabricant du roulement.
Durée de vie nominale d'un ensemble de roulements
L E 10 = [ (1 / L 1 10 )1,5 + (1 / L 2 10 )1,5 + ……  ] -1,5
Charge et vitesse variables
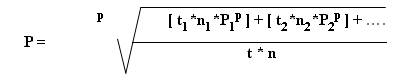
t i	Temps de fonctionnement sous P = cste et V = cste
t	Durée totale de fonctionnement
n i	Vitesses constantes correspondant respectivement aux temps t i
n	Vitesse moyenne sur la durée totale
P i	Charges constantes correspondant respectivement aux fraction de temps m i
p	3	pour les roulements et butées à billes
	10/ 3	pour les roulements et butées à rouleaux
Vitesse moyenne sur la durée totale
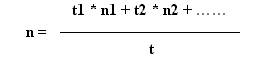
Charge linéairement variable et charge constante
P = ( P min + 2 * P max ) / 3
Mouvements oscillants
n = ( n osc * Ø ) / 180
n osc	nombre d'oscillations " Aller et Retour " par minute
Ø	Amplitude d'une oscillation " Aller " (en degrés)
Ne pas utiliser l'équation si l'angle d'oscillation est plus petit que le double du pas angulaire des éléments roulants : Risque de brinelling !